- A+
PokerStars亚洲版(PS281.COM)全球最大德州扑克平台。发牌公正，与世界玩家同台竞技
《The Mathematics of Poker》中文翻译
正态分布
当我们从一个分布中选取一个随机结果时，它输出的值必定是其隐含的分布中的某一个可取到的结果。我们称这样的一个值为随机变量。假设我们要扔一枚硬币。扔硬币的结果（正或反）就是一个随机变量。现在我们分别用数字1（代表正）和数字0（代表反）标记其输出结果。那么扔硬币的结果要么是1（50%的可能性）要么是0（50%的可能性）。如果我们扔多次硬币，并将其输出结果加总，那么我们就可以得到一个值，它代表了一系列随机变量输出结果的总和，我们称之为样本（“正，反，正，正，正，反，正”）。而样本值就是其样本背后对应的数字（“1，0，1，1，0，1”）。
现在我们扔100次硬币，并记录其中“正”出现的情况，也就是“1”出现的次数。这个样本的期望值为50，而每次的扔硬币的期望值为0.5。
而单次扔硬币的方差和标准差的计算如下：
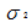=（1/2）（1-1/2）2+（1/2）（0-1/2）2=1/4
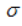=1/2
从之前的章节介绍中我们已经知道方差是可以加总的。
因此扔100次硬币的方差为25。
与单次扔硬币有标准差一样，一个扔硬币的样本也有其标准差。但是，与方差不同，标准差没有可加性。但是两者之间仍然有相关性。
对于N次实验，其方差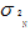
与单次实验的方差
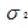有如下关系：
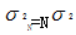
因此
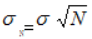
标准差的平方根关系是一个重要的结论，因为它向我们展现了标准差随着实验次数的增多是如何变化的。如果我们再一次扔硬币，其标准差为1/2，而如果我们扔100次，其标准差不是50，而是5，因为100的平方根是10。另一个显而易见的地方是，100次扔硬币的方差是25，而25的平方根是5，当然就是其标准差。
一个样本输出结果的分布就是一个概率分布，并被称为抽样分布。一个统计学的重要结论，中心极限定理，描述了抽样分布与其背后隐藏的概率分布的关系。中心极限定理告诉我们的是，随着样本数量的增加，样本结果的和的分布会逐渐趋向于一个特殊的分布---正态分布。
注：
本节一些内容可能有些难懂，因此我特意在此处对一些难点做一些解释，希望可以帮助大家理解，毕竟这节如果看不懂的话，之后的阅读会更难。
本节的第一个难点是“样本”与“样本值”。简单的说，“样本”就是扔若干次硬币后，把每次正、反的情况都记录下来的结果；而“样本值”就是以具体的数字对应各个“样本”，而有了具体数字之后，就可以做出数学方面的计算。
本节的第二个难点在于样本的标准差与方差的计算。上一节中已经介绍了方差与标准差的基本概念，其中已经介绍了单次实验的方差与标准差的计算，如果有忘记的读者可以再回顾一下。
上一节中还提到的一个概念就是“可加性”，简单的说，就是扔一百次硬币的方差，就是扔一次硬币的方差的100倍。但标准差是没有可加性的。那我们如何计算多次实验的方差呢？其实并不难，因为我们已经知道多次实验的方差如何计算了，而标准差其实就是方差的平方根。再结合文中给出的公式的话，相信现在大家已经可以理解样本方差与标准差的计算了。
本节的最后一个难点在于本节的最后一段话中的几个概念，也就是“抽样分布”、“中心极限定理”、以及“正态分布”。首先要注意一点，“抽样分布”与原概率分布是不同的，就以扔硬币为例，理论上我们是不可能得到它的真实的概率分布的，因为从定义上说，我们必须要进行无穷无尽次实验，才可以达到真实概率分布。而“抽样分布”的话，举个例子就是扔100次硬币，记录每次扔硬币的结果，以这些结果来推断真实的概率分布。当然一般情况下，样本越多，就越接近真实概率分布。在统计中，我们都是用“抽样分布”来估算真实概率分布的。而“中心极限定理”简单讲的就是随着样本量的增加，任何一个“抽样分布”的和分布都会逼近“正态分布”，这也就是正态分布为什么这么重要的原因了。在之后的几节中本书都会继续讲解正态分布方面的内容。
举报
+1
6UP-德扑第一平台&PokerStars亚洲唯一合作伙伴,新会员首存100送50元.
扑克之星亚洲版6UP官方网址：https://evp89.com
6UP扑克之星官网发布页：www.6updh.com
以上文章来源于网络，由6up扑克之星中文网整理发布
