- A+
PokerStars亚洲版(PS281.COM)全球最大德州扑克平台。发牌公正，与世界玩家同台竞技
《The Mathematics of Poker》中文翻译
统计学家绘制出了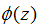
取值表，也设计了可以提取这些值的电子表格程序。在z=-1与z=1之间的面积大概为0.68；在z=-2与z=2之间的面积大概为0.955；在z=-3与z=3之间的面积大概为0.997。
这些取值意味着一个正态分布的样本取值遵循如下规律：
一个实例或许可以帮助我们理解这些规律。让我们再回到之前讨论的掷骰子游戏。掷一枚骰子，如果结果为1-5玩家会损失一个单位，如果结果为6玩家会得到6个单位。我们成这个新游戏位D2。
那么这个游戏的期望为：
<D2>=(5/6)(-1)+(1/6)(6)=1/6
当这个玩家获胜时，考察他偏离均值的程度，我们有：
Vwin=(6-1/6)2=（35/6）2
当这个玩家失败时，考察他偏离均值的程度，我们有：
Vlose=(-1-1/6)2=（-7/6）2
因此这个游戏的方差为：
VD2=p(win)(Vwin)+p(lose)(Vlose)=(1/6)（35/6）2+(5/6)（-7/6）2≈6.806
假设我们掷200次骰子，那么玩家总共可以赢下的单位的概率是多少呢？赢下超过40个单位是多少呢？影响超过100个单位的呢？
我们可以用我们刚刚学到的技术方法来解决上述问题。首先我们计算出200个样本的标准差，或者有时又可以称为标准误。其值为：
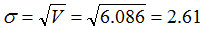
利用之前的计算样本标准误的公式我们可以得到：
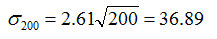
对于200次实验，其期望值，或者说均值，就是单次实验的期望乘以实验次数200，为33.33。用之前提到的z值计算方法，我们可以得到在0点的z值：
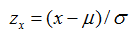
当x=0时，
Z0=(0-33.33)/36.89=-33.33/36.89=-0.9035
从任何一本统计书中的标准正态分布表我们都可以找到z值对应d概率，在这里ø(-0.9035)为0.1831，也就是说有18.31%的可能性玩家在200次实验后收益小于0。
而为了得到收益超过40单位的概率，我们首先要求出40对应的z值；
Z40=(40-33.33)/(36.89)=0.1807
ø(0.1087)=0.5717
但ø(0.1087)=0.5717表达的是取值在40左侧的概率，或者说收益不到40单位的概率。为了找到我们想求得的概率，或者说收益超过40单位的概率，我们必须求出1-ø(0.1087)。
1-ø(0.1087)=0.4283
因此有42.83%的可能性我们在200次实验后又超过40单位的收益。
相似地我们可以求出收益超过100单位的概率：
Z100=(100-33.33)/(36.89)=1.8078
ø(1.8078)=0.9646
p=1-ø(1.8078)=0.0354
也就是说200次实验后收益超过100单位的概率是3.54%。
附：
标准正态分布表
举报
+1
6UP-德扑第一平台&PokerStars亚洲唯一合作伙伴,新会员首存100送50元.
扑克之星亚洲版6UP官方网址：https://evp89.com
6UP扑克之星官网发布页：www.6updh.com
以上文章来源于网络，由6up扑克之星中文网整理发布
